행렬이란 무엇일까?
MATLAB에서 행렬(matrix)이란 numeric 타입 변수의 일종이다. 아래의 그림을 보면 다양한 numeric 타입들 간의 포함 관계를 확인할 수 있다.
위 그림에서 볼 수 있는 것 처럼 스칼라는 숫자 하나를 나타내고, 벡터는 스칼라를 여러개 일렬로 나열한 것이다. 이 개념을 확장하여 행렬은 벡터를 여러개 일렬로 나열한 것이라고 할 수 있다.
\[\text{scalar: } 3\text{, vector: } \begin{bmatrix} 3 \\ 2 \\ 5 \end{bmatrix}\text{, matrix:} \begin{bmatrix}3 & 1 & 2 \\ 2 & 3 & 2 \\ 5 & 7 & 9\end{bmatrix}\]행렬의 형태는 숫자들을 격자 모양의 2차원 평면에 나열한 것과 같은데 좌우 방향으로 나열된 숫자들 그룹을 “행(row)”이라고 하고, 상하 방향으로 나열된 숫자들의 그룹을 “열(column)”이라고 한다.
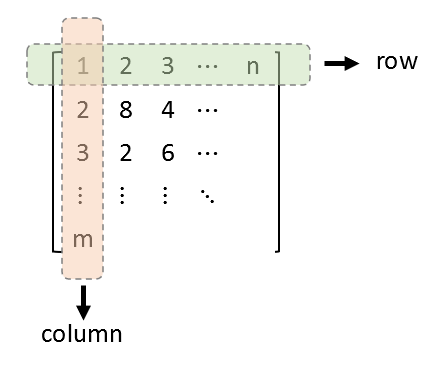
행렬의 크기를 말할 때 행과 열의 개수를 이용한다. 행의 개수가 m개, 열의 개수가 n 개인 행렬은 m 행, n 열 행렬 혹은 m by n 행렬이라고 부른다. 이와 같은 맥락으로 행렬을 만들 때는 행벡터, 열벡터를 만들 때의 방식을 그대로 이어나가서 대괄호와 콤마와 세미콜론을 이용해 행, 열을 구분해 행렬을 정의할 수 있다.
A = [1, 2; 3, 4]
A =
1 2
3 4
그러면 행렬을 굳이 배워야하는 이유는 무엇일까? 우선, 여러 데이터들을 다루는데 도움이 된다. 앞선 벡터 다루기 편에서는 벡터가 유용한 이유는 우리가 다루는 모든 데이터를 “벡터”의 단위로 쪼개 생각할 수 있기 때문이라고 언급했다. “데이터 취급 단위”인 벡터를 여러개 모아둔 행렬은 데이터들을 담아둔 하나의 폴더를 다루는 것과 같이 데이터들을 동시에 취급하여 다룰 수 있으므로 유용하다. 혹은 구조적으로 2차원의 형태인 데이터들을 다룰 때 행렬을 직접 사용할 수도 있다.
행렬을 이용하는 함수
벡터 다루기 페이지의 벡터를 이용하는 함수 챕터에서 다룬 함수들과 마찬가지로 MATLAB의 많은 함수들이 행렬을 입력으로 받을 수 있다. 행렬을 입력으로 받는 함수들은 크게 세 가지 방식 중 하나로 작동하는데, 1) 행렬 전체를 이용해 시각화하거나, 2) 행렬의 각 “열”을 각각의 벡터로 다루어 한꺼번에 처리하거나, 3) 행렬에 특화된 수학적 연산을 취해주는 기능을 수행한다.
행렬 전체를 이용해 시각화 하는 함수
행렬 자체를 이용해 시각화하는 함수들은 행렬 원소의 값들을 높이나 색깔로 다루어 시각화한다. 가령, imagesc 함수는 아래와 같이 색깔을 이용해 행렬을 이미지로 시각화한다.
A = [1, 2; 3, 4];
imagesc(A); colorbar;
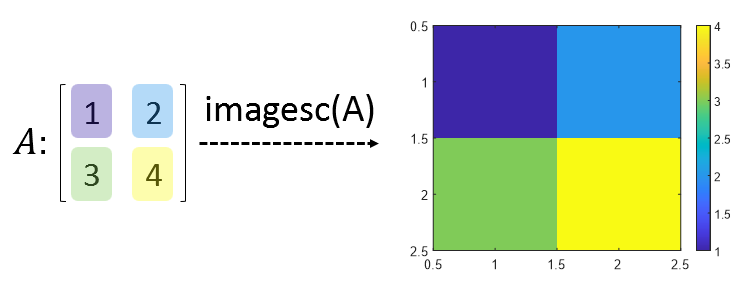
또, surf 같은 함수는 높이를 이용해 행렬을 이미지로 시각화한다.
[X,Y] = meshgrid(1:0.5:10,1:20);
Z = sin(X) + cos(Y);
surf(X,Y,Z)
행렬의 각 열을 각각의 벡터로 다루어 한꺼번에 처리하는 함수
MATLAB에서 벡터의 기본 방향은 열벡터(column vector)이다. 만약, 어떤 함수가 여러 벡터를 한꺼번에 처리하기 위해 행렬을 입력으로 받는다면, 이 함수는 각각의 열벡터들을 서로 다른 벡터로 취급하는 것이 디폴트로 보아야 한다. 예를 들면 plot 함수는 아래와 같이 행렬을 입력으로 받아 사용한다.
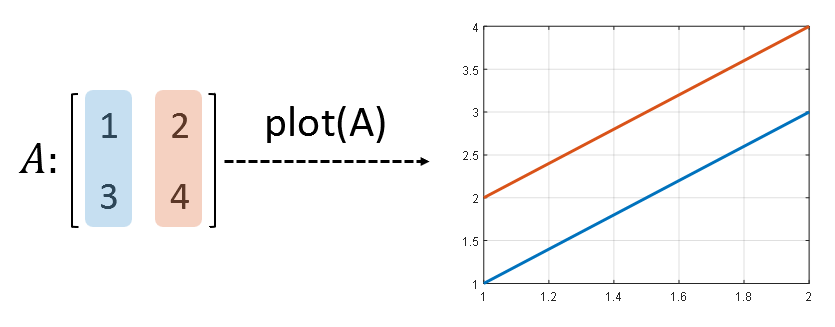
또, 예를 들어 “sum” 함수는 각 열별로 합을 구해준다.
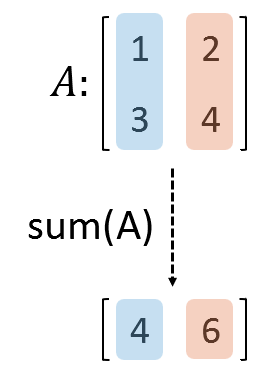
행렬에 특화된 수학적 연산을 취해주는 함수
덧셈
행렬에 대한 덧셈 연산은 각 위치의 원소별로 수행된다. 따라서, 원칙적으로는 크기가 같은 행렬끼리만 덧셈 연산을 수행해야 한다.
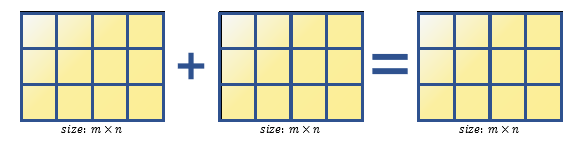
가령 아래와 같은 예시를 생각할 수 있다.
A = [1, 2; 3, 4];
B = [0, 1; 2, 3];
A + B
ans =
1 3
5 7
그런데, MATLAB에서는 implicit expansion이라는 기능이 있어 서로 크기가 다른 벡터/행렬 간에 덧셈 연산이 가능하다. 다만, 크기가 다른 벡터/행렬 간 덧셈 연산을 하는 경우 더해지는 두 개의 벡터/행렬이 한 개의 행 혹은 한 개의 열을 가져야 한다. 상당히 직관적이지만, 예상치 못한 결과를 불러올 수도 있으므로 계산 시 유의해야 한다. 대략 아래와 같은 세 가지 가능성이 존재한다.
- 행렬에 스칼라를 더하는 경우
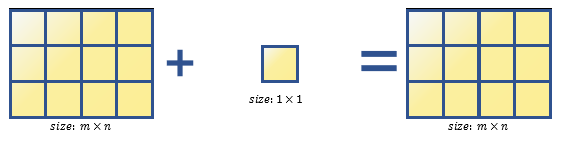
A = [1, 2; 3, 4];
b = 1;
A + b
ans =
2 3
4 5
- 행렬에 열벡터 혹은 행벡터를 더하는 경우
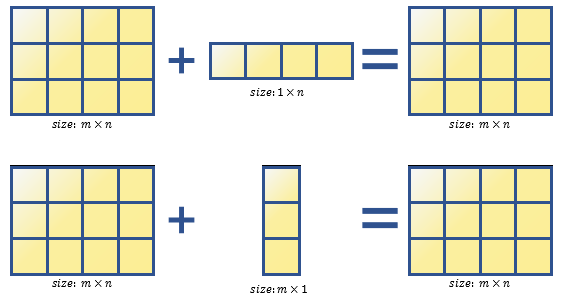
A = [1, 2; 3, 4];
b = [1, 2];
A + b
ans =
2 4
4 6
- 행벡터와 열벡터를 더하는 경우
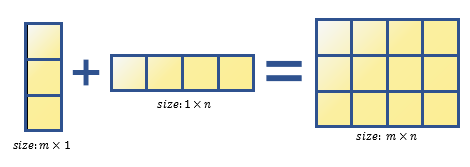
a = [1, 2];
b = [4; 5];
a + b
ans =
5 6
6 7
implicit expansion이 불가능한 경우는 아래와 같다.
- 더하고자 하는 행렬 중 하나의 차원이 1이 아닌 경우
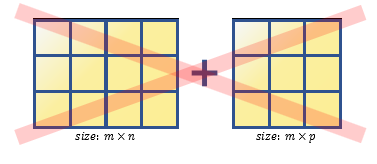
A = [1, 2; 3, 4; 5, 6];
B = [3 ,5 ,2 4; 1, 3, 2, 2];
A + B
Arrays have incompatible sizes for this operation.
- 크기가 맞지 않는 행벡터 혹은 열벡터 간의 덧셈
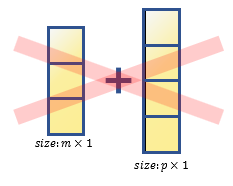
a = [1, 2, 3];
b = [2, 3, 4, 5];
a+b
Arrays have incompatible sizes for this operation.
이 내용에 관한 더 자세한 내용은 MathWorks 홈페이지에서 찾을 수 있다.
스칼라 곱하기/나누기
벡터/행렬에 스칼라를 곱하거나 나눌 때는 신경 쓸 것 없이 바로 나누어 주면 된다.
A = [1, 2; 3, 4];
c = 3;
A*c
A/c
ans =
3 6
9 12
ans =
0.3333 0.6667
1.0000 1.3333
행렬 간 곱셈
행렬 간 곱셈은 아래의 그림과 같이 계산된다. 왼쪽 행렬에서는 행, 오른쪽 행렬에서는 열을 가져와 내적한 결과를 결과물 행렬의 행, 열의 결과로 가져오게 되는 것이다.
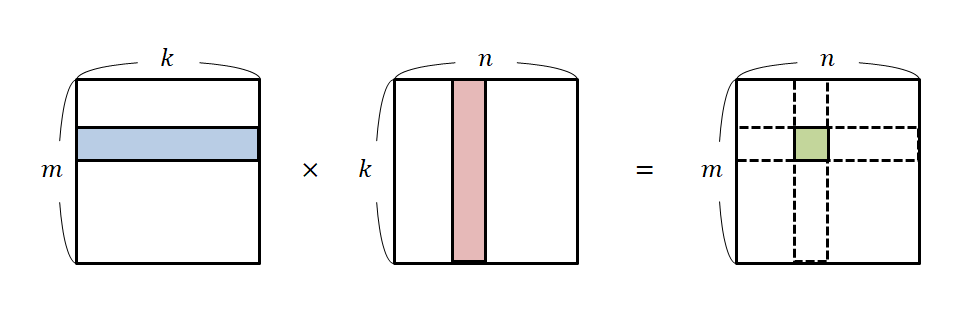</img>
수식으로 예를 들면 아래와 같다.
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\begin{bmatrix}a & b \\ c & d\end{bmatrix} = \begin{bmatrix} 1 \cdot a +2\cdot c & 1\cdot b + 2\cdot d \\ 3\cdot a + 4\cdot c & 3\cdot b + 4 \cdot d \end{bmatrix}\]만약 행렬 곱셈에 관해 잘 모르고 있다면 여기서 더 자세한 내용을 공부하여도 좋을 것 같다.
MATLAB은 이러한 행렬 곱셈을 쉽게 적용할 수 있게 설계되었다.
A = [1, 2; 3, 4];
B = [3, 2; 2, 5];
A * B
ans =
7 12
17 26
선형대수학 시간에 배우는 것이지만, 행렬 끼리의 곱을 수행할 때는 앞의 행렬의 열 개수와 뒤의 행렬의 행 개수가 같아야지만 연산이 가능하다. 다시 말해 아래와 같은 경우는 곱셈 연산이 수행될 수 없다.
A = [1, 2; 3, 4];
B = [1, 2; 3, 4; 5, 6];
A * B
Error using *
Incorrect dimensions for matrix multiplication. Check that the number of columns in
the first matrix matches the number of rows in the second matrix. To operate on each
element of the matrix individually, use TIMES (.*) for elementwise multiplication.
행렬 간 나눗셈 (역행렬)
행렬 나눗셈은 역행렬을 곱하는 과정과 동일한 것이라 할 수 있다. 역행렬을 곱한다는 것에 대해 조금 더 이해하기 위해서 아래의 예시를 살펴보자.
\[\begin{bmatrix} 8 & 1 & 6 \\ 3 & 5 & 7 \\ 4 & 9 & 2 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \end{bmatrix} = \begin{bmatrix}28 \\ 34 \\ 28\end{bmatrix}\]각 행렬 및 벡터들에 대응되는 심볼을 $A, x, b$라고 하여 아래와 같이 쓸 수 있다고 하자.
\[Ax = b\]그러면, $x$의 값을 구하기 위해선 양변의 왼쪽에 $A$의 역행렬을 곱해야 한다. 즉,
\[A^{-1}Ax = A^{-1}b\] \[x = A^{-1}b\]와 같이 계산할 수 있다. 여기서 $A^{-1}$을 곱하는 것을 행렬로 나눠준다고 표현한 것이다.
MATLAB에서는 백슬레쉬(＼)를 이용해 이 나눗셈을 표현할 수 있다. 한글 윈도우에서는 백슬레쉬가 원화 모양(￦)으로 나오기 때문에 왜 원화 모양을 가지고 나눗셈을 표현했나 의아하기도 할 수 있지만 $A^{-1}$가 왼쪽에 붙는다는 사실을 생각해보면 $A$가 분모로 가는 분수와 같은 형태를 생각해볼 수 있을 것이다.
사진 출처: Cleve’s Corner: Cleve Moler on Mathematics and Computing (MathWorks)
A = [8, 1, 6; 3, 5, 7; 4, 9, 2];
b = [28; 34; 28];
x = A\b
x =
1
2
3
행렬 원소 조작하기
행렬 원소 인덱싱
행렬 원소의 인덱싱은 행과 열을 함께 이용해야 한다. 아래의 그림을 통해 어떤 방식으로 행렬의 indexing이 수행되는지 알아보자.
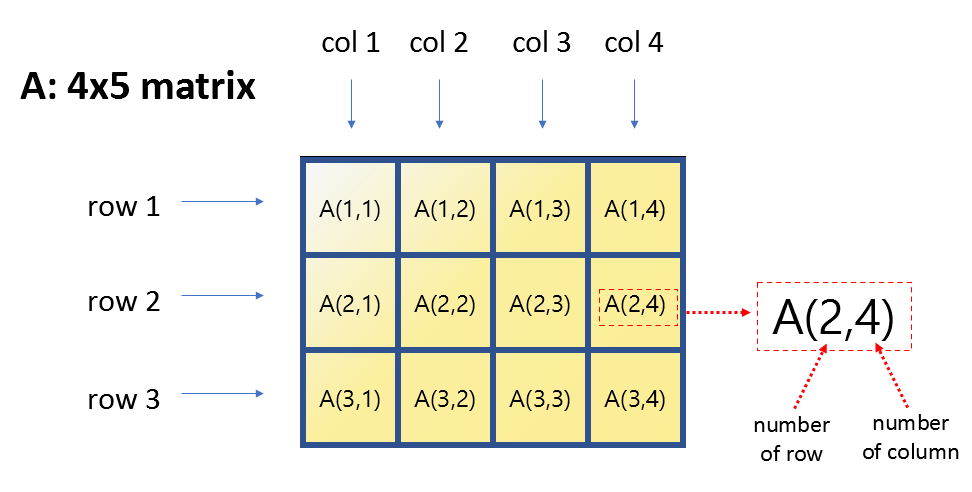
행렬 원소 꺼내보기
예를 들면 아래와 같이 A 행렬의 2행, 3열의 원소를 얻어낼 수 있다.
A = magic(4)
A(2, 3)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
ans =
10
위의 예시를 보면 A의 2행, 3열에 존재하는 값을 불러오기 위해 A(2, 3)과 같이 입력한 것을 알 수 있으며 10이라는 원소값이 출력된 것을 알 수 있다.
만약, 행렬의 특정 행 혹은 열 전체를 꺼내고 싶은 경우에는 아래와 같이 콜론(“:”)을 사용할 수 있다.
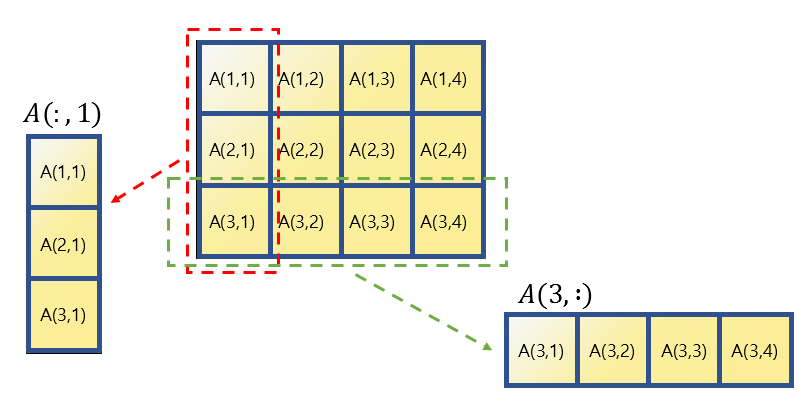
아래와 같이 A(1,:)이라고 입력하면 1행과 그에 대응하는 열 전체를 의미하게 된다.
A = magic(4)
A(1, :)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
ans =
16 2 3 13
또 만약 아래와 같이 A(:, 1)이라고 입력하면 1열에 대응하는 원소들을 모두 꺼내게 된다.
A = magic(4)
A(:, 1)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
ans =
16
5
9
4
행 혹은 열 제거하기
행렬의 행 혹은 열을 제거하기 위해선 벡터에서 수행했던 것 처럼 원하는 행에 빈 벡터를 집어 넣으면 된다.
아래의 예시에서는 1열을 제거해보았다.
A = magic(4)
A(:, 1) = []
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
A =
2 3 13
11 10 8
7 6 12
14 15 1
또 아래 예시에서는 1행을 제거해보았다.
A = magic(4)
A(1, :) = []
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
A =
5 11 10 8
9 7 6 12
4 14 15 1
행렬 합치기
행렬을 합칠 때에도 벡터를 합칠 때와 마찬가지로 대괄호를 이용해 두 행렬을 묶어주면 된다.
A = magic(3);
B = eye(3); % 3x3 identity matrix
[A, B]
ans =
8 1 6 1 0 0
3 5 7 0 1 0
4 9 2 0 0 1
특수 행렬을 만드는 함수
몇 가지 특별한 행렬들을 만들기 위한 함수들이 마련되어 있다. 아래와 같은 명령어들을 MATLAB Command Window에 입력해보자.
zeros
“zeros” 함수는 0으로만 구성된 행렬을 출력해준다. “zeros(a, b)”는 a 행, b 열의 크기로 구성된 원소가 0으로만 채워진 행렬을 출력해준다.
a = zeros(5, 5)
a =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
ones
“ones” 함수는 1로만 구성된 행렬을 출력해준다.
a = ones(5, 5);
a =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
가끔, “그럼 2, 3 등으로 채워진 행렬도 존재하나요?” 라는 질문을 받기도 하는데, 그런 함수는 없다. 다만, 아래와 같은 방식으로 응용하면 3으로 채워진 행렬을 얻을 수 있을 것이다.
a = 3 * ones(5, 5);
a =
3 3 3 3 3
3 3 3 3 3
3 3 3 3 3
3 3 3 3 3
3 3 3 3 3
eye
선형대수학에서 사용되는 단위 행렬(identity matrix)를 출력해주는 함수도 있다.
identity = eye(5, 5)
identity =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
magic
또, 마방진 행렬도 존재한다. 이 행렬은 “아무 행렬”이나 써먹고 싶지만 0 또는 1로만 구성된 행렬을 사용하고 싶지는 않을 때 주로 사용한다. n x n 마방진 행렬은 1부터 n^2까지의 숫자를 모두 채워서 어떤 행이나 열, 그리고 대각 성분을 다 더하더라도 합이 같게 만든 행렬이다. 가령, 3x3 마방진 행렬은 어떤 행이나 어떤 열 혹은 대각 성분의 원소를 모두 더하더라도 15라는 값이 나온다는 것을 알 수 있다.
m = magic(3)
m =
8 1 6
3 5 7
4 9 2
rand & randn
랜덤 변수를 원소로 갖는 행렬도 존재한다. “rand” 0에서 1사이에서 정의된 uniform distribution 으로부터 얻는 랜덤 변수를 원하는 크기의 행렬에 표시해준다. 또, “randn” 함수는 표준정규분포에서 얻는 랜덤 변수를 원하는 크기의 행렬에 표시해준다.
rm1 = rand(3, 3)
rm2 = randn(3, 3)
rm1 =
0.7922 0.0357 0.6787
0.9595 0.8491 0.7577
0.6557 0.9340 0.7431
rm2 =
-0.3034 0.8884 -0.8095
0.2939 -1.1471 -2.9443
-0.7873 -1.0689 1.4384
벡터/행렬을 다룰 때 사용하는 대표적인 함수들
마지막으로 행렬을 다룰 때 유용하게 쓸 수 있는 내장 함수들을 몇 가지 알아보도록 하자. 각 함수들에 관한 아주 간단한 설명과 사용 예시들을 작성하였다. 이 함수들에 관한 더 자세한 사항은 “help” 혹은 “doc” 명령어를 통해 직접 확인해보도록 하자. 이번 페이지에서 다 외우지 말고 한번 훑어본 뒤 다음에 필요할 때 또 찾아보면서 천천히 본인의 것으로 만들도록 하자.
벡터/행렬의 최솟값(min)
벡터/행렬의 최솟값을 반환해준다.
min([9, 1, 8, 4, 5])
ans =
1
만약, 좌변에 출력 두개를 사용할 경우 위치까지도 반환해준다.
[min_val, min_idx] = min([9, 1, 8, 4, 5])
min_val =
1
min_idx =
2
최소값은 1이고 그 값은 행렬의 두 번째 값이라는 의미이다.
만약, “min” 함수에 행렬이 들어갈 경우 각 열의 최솟값을 반환해준다.
min([8, 1, 6; 3, 5, 7;4, 9, 2])
ans =
3 1 2
벡터/행렬의 최댓값(max)
벡터/행렬의 최댓값을 반환해준다.
max([9, 1, 8, 4, 5])
ans =
9
만약, 좌변에 출력 두개를 사용할 경우 위치까지도 반환해준다.
[max_val, max_idx] = max([9, 1, 8, 4, 5])
max_val =
9
max_idx =
1
최소값은 9이고 그 값은 벡터의 첫 번째 값이라는 의미이다.
만약, “min” 함수에 행렬이 들어갈 경우 각 열의 최솟값을 반환해준다.
max([8, 1, 6; 3, 5, 7;4, 9, 2])
ans =
8 9 7
벡터/행렬의 크기(size)
행렬의 행, 열 개수를 반환해준다.
size(magic(3))
ans =
3 3
벡터/행렬의 길이(length)
행렬의 길이를 반환해준다. 앞의 “size” 함수에서 나온 결과의 최댓값과 같은 결과를 출력한다.
length(magic(3))
ans =
3
벡터/행렬 원소의 개수(numel)
모든 원소의 개수를 반환해준다. “size” 함수에서 나온 결과의 모든 원소값들을 곱한 것과 같다.
numel(magic(3))
ans =
9
전치 연산(transpose, ‘)
전치 연산을 취해준다. 행과 열을 바꾸는 결과를 얻게 된다. 여기서 “ ‘ “ 은 세미콜론 옆에 있는 단따옴표이다.
transpose([3, 4])
[3, 4]'
ans =
3
4
ans =
3
4
상하 방향 뒤집기(flipud)
위 아래 방향으로 행렬의 원소를 뒤집어준다. 가령 아래와 같은 식이다.
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\rightarrow \begin{bmatrix} 3 & 4 \\ 1 & 2 \end{bmatrix}\]flipud([1, 2; 3, 4])
ans =
3 4
1 2
좌우 방향 뒤집기(fliplr)
좌우 방향으로 행렬 원소를 뒤집어준다. 가령 아래와 같은 식이다.
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\rightarrow \begin{bmatrix} 2 & 1 \\ 4 & 3 \end{bmatrix}\]flipud([1, 2; 3, 4])
ans =
2 1
4 3
대각성분 벡터/대각행렬 생성 (diag)
입력이 행렬일 경우 대각 성분으로 구성된 벡터를 출력해주고, 입력이 벡터인 경우 해당 벡터의 성분이 대각 성분에 위치한 행렬을 생성해준다.
% 입력이 행렬인 경우
magic(5)
diag(magic(5))
% 입력이 벡터인 경우
diag([1,2,3])
ans =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
ans =
17
5
13
21
9
ans =
1 0 0
0 2 0
0 0 3
벡터/행렬 재배열 (reshape)
행렬의 크기를 변경시켜준다. 다만, 원소가 더해지거나 사라지지는 않는다. 또, MATLAB에서 행렬의 indexing은 선형적인 indexing으로 생각했을 때 열방향이라는 점을 꼭 명심하자.
아래의 예시를 살펴보자.
reshape([1,2,3,4,5,6], 2, 3)
ans =
1 3 5
2 4 6
즉, 첫 번째 입력으로 넣은 벡터/행렬을 두 번째, 세 번째 입력으로 넣은 행, 열의 크기 만큼으로 바꿔준 것이다.
\[\begin{bmatrix}1&2&3&4&5&6\end{bmatrix}\rightarrow \begin{bmatrix}1&3&5 \\ 2 & 4& 6\end{bmatrix}\]벡터/행렬 복제하여 붙여넣기 (repmat)
행렬을 복제해서 원하는 행, 열의 구조에 맞춰 복사 붙여넣기를 해준다.
repmat([1,2; 3,4], 2, 2)
ans =
1 2 1 2
3 4 3 4
1 2 1 2
3 4 3 4
합계 (sum)
행렬의 각 열별로 행방향 합을 구해준다.
a = [1,2; 3,4];
sum(a)
ans =
4 6
평균 (mean)
행렬의 각 열별로 행방향 평균을 구해준다.
a = [1,2; 3,4];
mean(a)
ans =
2 3
중위값 (median)
벡터의 중위값을 계산해준다. 행렬에 사용할 경우 각 열별로 행방향 중위값을 계산해준다.
a = [1, 2, 7, 9, 1 ,4, 3, 4, 5, 1, 2];
median(a)
ans =
3
오름차순 정렬 (sort)
벡터 원소를 오름차순으로 정렬해준다. 위 “중위값” 설명 부분에서 a를 오름차순 정렬해보면 3이 중위값임을 알 수 있다.
a = [1, 2, 7, 9, 1 ,4, 3, 4, 5, 1, 2];
sort(a)
ans =
1 1 1 2 2 3 4 4 5 7 9
0이 아닌 값의 인덱스 찾기 (find)
설명 그대로 0이 아닌 값이 몇 번째 원소인지 알려준다.
a = [1, 0, 4, 0, 0, 3];
find(a)
ans =
1 3 6
find 함수는 “==” 연산자와 함께 사용하는 경우가 많다. “==” 연산자는 양 옆의 숫자가 같은지 판단해주는 연산자이다. 가령, 아래와 같이 입력하면 세 번째 원소인 4만 참이고 나머지는 거짓으로 판단한다. logical 데이터 타입에 관해서는 이 페이지에서 더 자세하게 다룰 예정이다.
a = [1, 0, 4, 0, 0, 3];
a == 4
ans =
1×6 logical array
0 0 1 0 0 0
따라서, 위 “ans” 결과에 find를 함께 사용하면 참으로 출력된 벡터 인덱스인 “3”만 나오게 되는 것이다.
a = [1, 0, 4, 0, 0, 3];
find(a == 4)
ans =
3